River-Delta Oriented Programming

A lattice-based approach to data composition

image

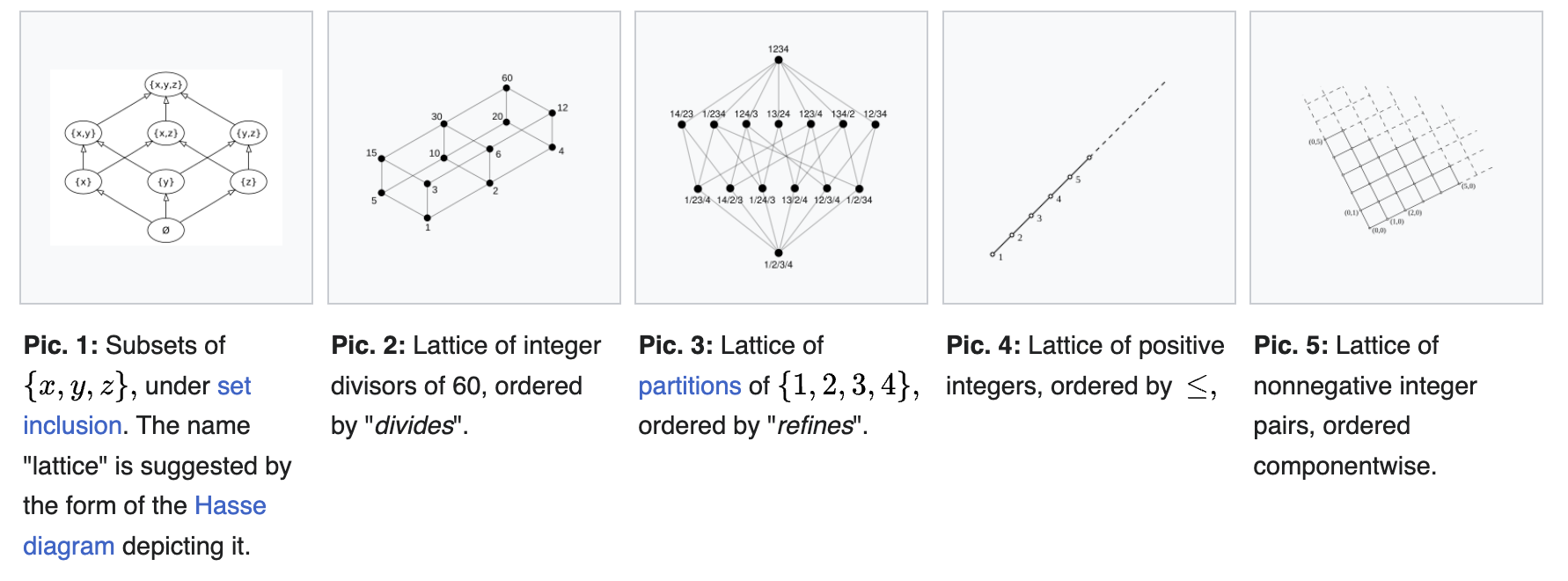
The term river-delta is coined here to create a memorable and unthreatening real-life analogy for mathematical lattices: the different rivers of the river-delta all ultimately join into a single river stream, just like the elements of a (finite) lattice all ultimately join into a top element. image

There already exist a few good articles (1, 2) presenting the mathematical foundations of lattices in a digestible way for non-mathematicians. The goal of this article is to supplement them by first situating lattices among other algebraic structures and relating them to other programming constructs that you use, and then by sharing real world examples of lattice-based systems that programmers use everyday, probably without realizing it.

From Railways to River-Deltas

Lattices (river-deltas) are to safe data composition what monads (railways) are to safe control-flow composition.

The railway-oriented programming analogy has helped me assimilate the concepts behind monadic programming. I’m hoping that the river-delta oriented programming analogy that I am coining in this article will similarly help people learn about CRDTs and other useful applications of lattices.

The river-delta/lattice analogy emphasizes convergence/refinement rather than transformation/sequencing from railways/monoids. This important distinction will hopefully become clearer as you read through this article, but let’s start with a teaser example to anchor readers into a more concrete example.

From Monoids to Semilattices

Monoids are to reducing lists what semilattices are to merging concurrent state updates.

Practically speaking, monoids arise naturally because they represent the minimal amount of structure needed to perform a fold/reduce operation.

Monoids solve: “How do I combine a bunch of values in sequence?”

-- Reducing a list sequentially
sum [1,2,3,4] = 1 + 2 + 3 + 4 = 10
mconcat ["hello", " ", "world"] = "hello world"

Semilattices solve: “How do I merge two (concurrently achieved) states safely?” (think of an automated git conflict resolution)

-- Merging states from different replicas
replica_A_state V replica_B_state = merged_consistent_state
{user1_edits} U {user2_edits} = {all_edits_resolved}

Although these look very similar on the surface, they have completely different algebraic properties (see the theory section below), which leads to very different use-cases.

Theory

Taking a step back, it will be important to situate lattices in the world of mathematical structures and programming concepts. Readers should free to skip to the practical examples sections and come back here afterwards.

Lattices as Algebraic Structures

Lattices can be defined in two equivalent ways, either as a partially ordered set (poset) or as an algebraic structure. Feel free to read wikipedia as well as the articles references at the beginning of this article for their formalism. I will rather concentrate on how they compare and related to other more well-known algebraic structures, of which there are 6 major categories:

Groups (elliptic curves), Rings (integers), and Fields (Real/Complex numbers) are the most well known structures. We focus instead on semilattices and lattice-like structures.

Semilattices vs Monoids

In the structures with 1 set and 1 binary operation, semilattices (basically “half” of a lattice) are distinguishable from all the group-like structures by idempotency.

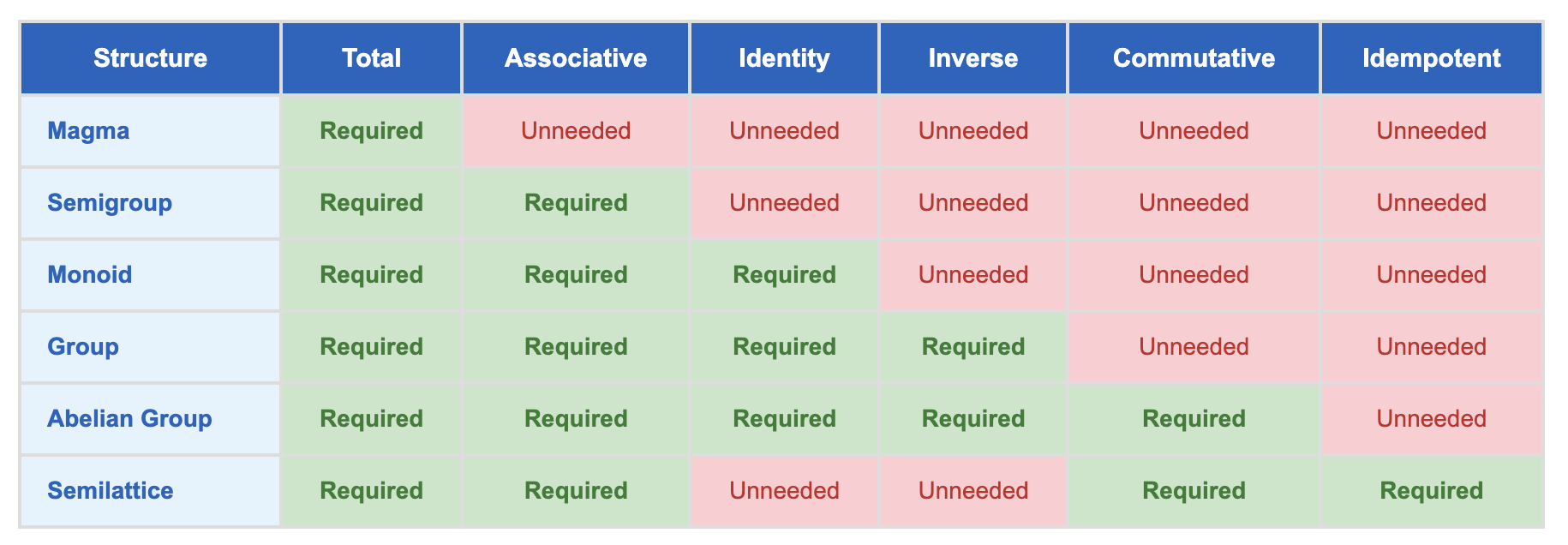
image

The binary operation of a lattice is for this reason typically called either meet or join, as opposed to plus or mult typically used in group-like structures.

-- Semigroup: only associativity required
class Semigroup a where
  (<>) :: a -> a -> a
  -- Law: (a <> b) <> c = a <> (b <> c)

-- Monoid: semigroup + identity element
class Semigroup a => Monoid a where
  mempty :: a
  -- Laws:
  --   Associative: (a <> b) <> c = a <> (b <> c)  [from Semigroup]
  --   Left identity:  mempty <> a = a
  --   Right identity: a <> mempty = a

-- Semilattice: semigroup + commutativity + idempotency
class Semigroup a => Semilattice a where
  -- No additional operations needed - the laws do the work!
  -- Laws: 
  --   Associative: (a <> b) <> c = a <> (b <> c)  [from Semigroup]
  --   Commutative: a <> b = b <> a                [new law]
  --   Idempotent:  a <> a = a                     [new law]

The philosophical difference is that lattice join is about finding the “best common ancestor” in a hierarchy, while monoid append is about sequential combination. Even when a monoid is used for “merging”:

Lattices vs Rings/Fields

In the structures with 1 set and 2 binary operations, the ring-like objects and lattice-like objects can be clearly distinguished. In the case of ringoids, the two operations (plus and add) are linked by the distributive law; in the case of lattices, the two operations (meet and join) are linked by the absorption law.

The distinction here is not that important, or at least I have not found a way to relate them meaningfully. The more important part is to understand that a lattice is an extension of a semilattice that allows going in the “reverse” direction: given sets, one can take their union to grow them, or their intersection to reduce them. Some applications like CRDTs and merging states only require going in one direction, but more complex applications like CUE and type lattices requires searching/inferencing over both operations of the lattice.

How does this relate to Monads and Railroads?

Note that despite the concise oft chanted phrase “a monad is a monoid in the category of endofunctors”, in practical programming use-cases a monad is drastically different from a monoid. As we saw above, monoid are, just like semilattices, about data. Comparatively, the category theoretical functor/applicative/monad concepts are about composing functions (or in programming about effectful computation). This distinction is made obvious by looking at their types:

image

Historical precursor to Category Theory

Comparatively to lattice theory, category theory is more broadly known to programmers, as can be seen by the wide range of applied articles [1 2 3]. This makes sense given that every programmer has to deal with functions, errors, and their composition. Comparatively fewer programmers ever get to compiler or database internals.

Nonetheless, as a mathematical subject, Category Theory came as a successor to Lattice theory:

McLane worked around 1930-35 in matroid lattices and semimodularity (exchange axioms); when he invented categories, his interest in lattices had waned out, and he considered lattice theory a too specialized subject with too specialized questions.

Corry’s book Modern Algebra and the Rise of Mathematical Structures that describes the historical transition from early “structuralism”, including Ore’s lattice-based approach, to categories.

The algebraic/poset properties of Lattices gives them a unique perspective useful to programming with data, which is why it is useful to study them outside of the more abstract category theory perspective.

Lattice Applications

We explore computer-science use cases for lattices. Given the TLDR that “lattices are for safe data composition”, it should come as no surprise that lattices have applications in databases, config DSLs, compilers and logic programming.

1. CRDTs (eventually consistent databases) and ACI

Conflict-free Replicated Data Type (CRDTs) have a long history. Afaiu, they became popular in the noSQL days when eventual consistency was becoming a thing, and were successfully used at scale by Amazon in their dynamo (not dynamoDB!) key-value store. Marc Shapiro’s group formalized them in 2011, and more recently Martin Kleppmann has further popularized them and solved some breakthroughs in their usage for collaborative editing.

Joe Hellerstein’s group at Berkeley, famous for the CALM conjecture (Consistency As Logical Monotonicity) has made further deep connections between lattices, logic programming, and CRDTs:

Designing a CRDT centers around providing a function to merge any two replicas, with the requirement that this single function is associative, commutative and idempotent (ACI), and defining atomic operations that clients can use to update a replica.

Classic anomalies in eventually consistent systems are caused by reordered, duplicated, or late-arriving updates, which CRDTs prevent using the 3 ACI properties:

  1. Associativity: late-arriving (can compute partial results, enables tree-reduction across nodes)
  2. Commutativity: reordered (removes need for buffering, allows packet spraying)
  3. Idempotency: duplicated (don’t need exactly-once delivery)

At the cost of more contrived state space (not every data structure can be made into a CRDT) and some non-trivial user-space code, CRDT-based systems can be made much faster because they don’t require expensive and slow consensus, nor sophisticated networking primitives like exactly-once delivery. They don’t even need TCP to buffer and reorder packets, and can instead spray UDP packets at the speed of the network links.

2. CUE (config language)

Given that config is data, it should come as no surprise that lattices could play a role in large scale configuration management. This is exactly that CUE was invented for; see this beautifully crafted explanation of the history of and reasoning for CUE, written by its creator Marcel van Lohuizen, who previously worked on K8s and BCL (Borg Config Lang) at Google.

The logic of CUE also goes into more mathematical details.

Issues with config inheritance

Linking back to our introductory teaser, inheritance forms a (non-commutative) monoid, aka sequential composition of configs:

child = parent ∘ overrides

Note that this operation is associative, but neither commutative nor idempotent (making it A instead of ACI). The fundamental problem is that inheritance conflates two different operations:

  1. Extension (adding new fields) - commutative + idempotent
  2. Override (changing existing values) - this is neither

Lattice-based Unification

CUE’s unification handles extension cleanly, while allowing for some constrained level of override: one can only override a value by a JOIN operation, which amounts to refining the value with a more fine-grained type in the type lattice. For example, one can refine int to [3,8], and further refine [3,8] to 5. But one cannot “override” int with string, or [3,8] with [2,4], or 5 with 8.

Most people are familiar with composition over inheritance; in the world of configs, one should say “lattice-based unification over inheritance”. Lattice-based unification forms a more constrained structure (meet-semilattice or bounded lattice) with additional properties that make composition more predictable and maintainable.

The key insight is that while both are valid algebraic structures, the additional properties of commutativity and idempotency in CUE’s approach lead to better engineering properties like:

3. Type and Subsumption Lattices (compilers)

Compiler implementation details are outside of my day-to-day activities, but learning of the applications of lattices inside them was not that surprising. After all, CUE does unify types and values into a lattice, so it makes a ton of sense that types on their own would form a lattice (which can be represented as an optimized bitset).

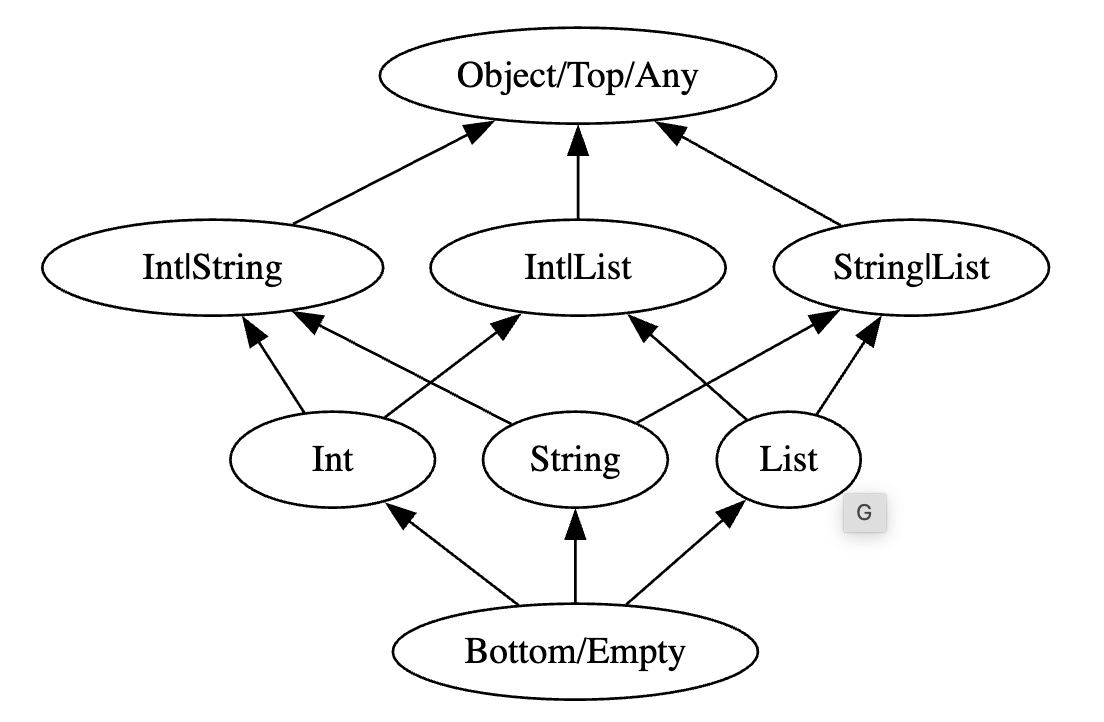
image

Type lattices are used for dataflow analysis in SSA compilers. Similar datastructures are also used: inference lattice in Julia, and Subsumption lattices in automated theorem proving and logic programming (e.g. prolog’s unification algorithm).

4. Lattice-based Crypto (post-quantum)

This application is even more outside of my knowledge zone. It feels very different quantitatively from all the other applications, but something tells me there are probably deep and fundamental ties between them. Would love to hear/learn more from anyone who knows about these connections.

Otherwise I plan on eventually learning about lattice-based cryptography and Learning with Errors (see this and this), and will then update this section. This feels especially pressing now that Bitcoin is in danger.